Etude du ressort uniquement (oscillations non-amorties) :
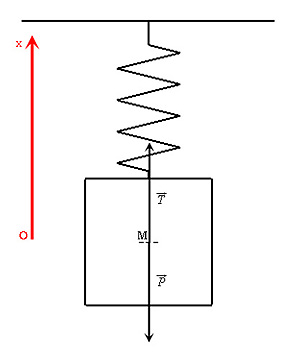
Les normes des vecteurs ne sont pas à l’échelle pour un question de lisibilité.
D’après la seconde loi de Newton (théorème du centre d’inertie) :
Dans un référentiel galiléen , la somme des forces extérieures appliquées à un solide est égale au produit de la masse du solide par l'accélération 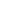 de son centre d'inertie M : de son centre d'inertie M :
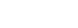
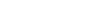
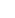 : force de tension appliquée au centre d’inertie de l’objet en Newtons : force de tension appliquée au centre d’inertie de l’objet en Newtons
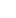 : poids de l’objet en Newtons : poids de l’objet en Newtons
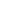 : masse de l’objet en kg : masse de l’objet en kg
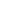 : accélération en : accélération en 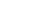
En projetant sur l’axe 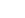 , on peut écrire la relation suivante : , on peut écrire la relation suivante :
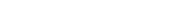
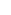 : constante de raideur du ressort : constante de raideur du ressort 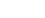
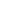 : allongement du ressort par rapport à sa position d’équilibre : allongement du ressort par rapport à sa position d’équilibre
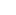 : allongement du ressort lorsque celui-ci est à l’équilibre : allongement du ressort lorsque celui-ci est à l’équilibre
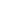 : accélération de la pesanteur à la surface de la terre en : accélération de la pesanteur à la surface de la terre en 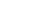
Or à l’équilibre, on a 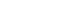 d’où d’où 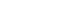 soit soit 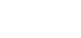
On obtient donc une équation différentielle du second ordre à coefficients constants et sans second membre.
Etude du système d’amortisseur (oscillations amorties) :
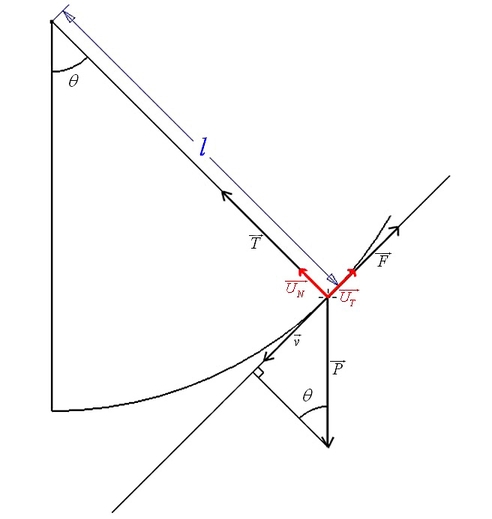
(Ce schéma illustre le système d’amortissement étudié lors de notre expérience)
Les normes des vecteurs ne sont pas à l’échelle pour un question de lisibilité.
D’après la seconde loi de Newton (théorème du centre d’inertie) :
Dans un référentiel galiléen , la somme des forces extérieures appliquées à un solide est égale au produit de la masse du solide par l'accélération 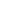 de son centre d'inertie M : de son centre d'inertie M :
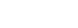
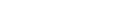
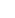 : force de tension appliquée au centre d’inertie de l’objet en Newtons : force de tension appliquée au centre d’inertie de l’objet en Newtons
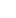 : poids de l’objet en Newtons : poids de l’objet en Newtons
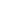 : force de frottements exercées sur l’objet en Newtons : force de frottements exercées sur l’objet en Newtons
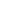 : masse de l’objet en kg : masse de l’objet en kg
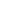 : accélération en : accélération en 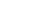
On associe au schéma une base appelée base de Frenet. Il s’agit d’un repère mobile ayant les caractéristiques suivantes :
- l’origine est le point mobile M. L’origine se déplace donc en fonction du temps.
- Le vecteur unitaire 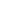 , tangent à la trajectoire, passant par le centre d’inertie M du mobile considéré comme ponctuel. Ce vecteur est orienté arbitrairement (pas nécessairement dans le sens du mouvement). , tangent à la trajectoire, passant par le centre d’inertie M du mobile considéré comme ponctuel. Ce vecteur est orienté arbitrairement (pas nécessairement dans le sens du mouvement).
- Le vecteur unitaire 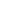 est normal à la trajectoire. Il est orienté vers l’intérieur de la courbe. est normal à la trajectoire. Il est orienté vers l’intérieur de la courbe.
On obtient donc : 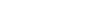
Avec 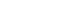 et et 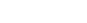
L’accélération tangentielle s’exprime par 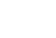
L’accélération normale s’exprime par 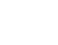 , , 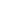 étant le rayon de courbure de la trajectoire. étant le rayon de courbure de la trajectoire.
En conclusion, on a : 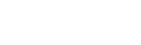
Par projection sur 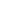 : :
On a : 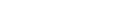
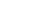 car toujours orthogonal à car toujours orthogonal à 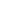
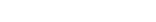
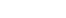 or or 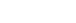 et et 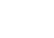 donc donc 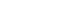 avec avec 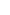 le coefficient de frottement. le coefficient de frottement.
Ce qui donne : 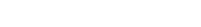 ou ou 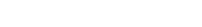 (1) (1)
Lorsque l’on travaille sur de faibles oscillations ( inférieures à 10° comme c’est le cas dans notre expérience), on peut assimiler 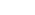 à à 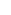 si l’on prend la mesure en radians. si l’on prend la mesure en radians.
On divise (1) par 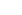 : : 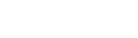
On obtient donc une équation différentielle du second ordre à coefficients constants et sans second membre.
Détermination du régime critique :
(pour une analyse plus approfondie, voir la page sur les )
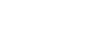
Dans le cas du régime critique, on a 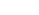
Soit 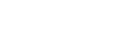
Si 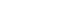 le régime est dit pseudo périodique (les oscillations dans ce cas sont dites oscillations libres amorties) le régime est dit pseudo périodique (les oscillations dans ce cas sont dites oscillations libres amorties)
Si 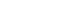 le régime est alors apériodique (frottements trop importants pour permettre au système d’osciller). le régime est alors apériodique (frottements trop importants pour permettre au système d’osciller).
Par projection sur 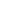 : (utile pour calculer la valeur de la tension aplliquée au solide). : (utile pour calculer la valeur de la tension aplliquée au solide).
On a : 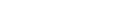
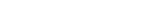
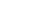 car toujours orthogonal à car toujours orthogonal à 
Ce qui donne 
On suppose alors que le mobile M est lancé sans vitesse initiale d’une hauteur 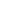 . .
D’après le théorème de l’énergie cinétique : la variation de l’énergie cinétique d’un solide, entre deux instants, est égale au travail des forces appliquées au solide entre ces deux dates, c’est à dire : 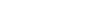
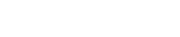
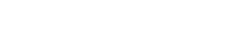
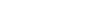 et et 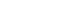
D’où 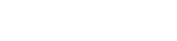
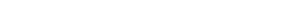
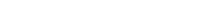
Exemple :
Si 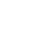 et et 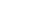 alors alors 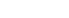
|



